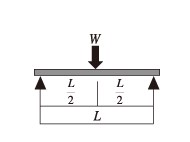
中央集中荷重の場合
\[
M(x)=
\begin{cases}
\dfrac{W}{2}x & (0 \leq x \leq \dfrac{L}{2})
\\
\dfrac{W}{2}(L-x) & (\dfrac{L}{2} \leq x \leq L)
\end{cases}
\\[30pt]
\ \ \theta(x)=
\begin{cases}
\dfrac{1}{EI}(\dfrac{W}{4}x^2+C_{1}) & (0 \leq x \leq \dfrac{L}{2})
\\
\dfrac{1}{EI}[-\dfrac{W}{4}(L-x)^2+C_{2}] & (\dfrac{L}{2} \leq x \leq L)
\end{cases}
\\[30pt]
\ \ \delta(x)=
\begin{cases}
\dfrac{1}{EI}(\dfrac{W}{12}x^3+C_{1}x+C_{3}) & (0 \leq x \leq \dfrac{L}{2})
\\
\dfrac{1}{EI}[\dfrac{W}{12}(L-x)^3-C_{2}(L-x)+C_{4}] & (\dfrac{L}{2} \leq x \leq L)
\end{cases}
\]
となり、境界条件より
\[
\delta(0)=C_{3}=0
\\
\delta(L)=C_{4}=0
\\
\theta(\dfrac{L}{2})=\dfrac{1}{EI}(\dfrac{WL^2}{16}+C_{1})=\dfrac{1}{EI}(-\dfrac{WL^2}{16}+C_{2})
\\
\ \ \rightarrow
C_{1}-C_{2}=-\dfrac{WL^2}{8}
\\
\delta(\dfrac{L}{2})=\dfrac{1}{EI}(\dfrac{WL^3}{96}+\dfrac{C_{1}L}{2})=\dfrac{1}{EI}(\dfrac{WL^3}{96}-\dfrac{C_{2}L}{2})
\\
\ \ \rightarrow
C_{1}+C_{2}=0
\\
\ \ \rightarrow
C_{1}=-\dfrac{WL^2}{16}\quad C_{2}=\dfrac{WL^2}{16}
\]
よって
\[
\theta(x)=
\begin{cases}
\dfrac{1}{EI}(\dfrac{W}{4}x^2-\dfrac{WL^2}{16}) & (0 \leq x \leq \dfrac{L}{2})
\\
\dfrac{1}{EI}[-\dfrac{W}{4}(L-x)^2+\dfrac{WL^2}{16}] & (\dfrac{L}{2} \leq x \leq L)
\end{cases}
\\[30pt]
\delta(x)=
\begin{cases}
\dfrac{1}{EI}(\dfrac{W}{12}x^3-\dfrac{WL^2}{16}x) & (0 \leq x \leq \dfrac{L}{2})
\\
\dfrac{1}{EI}[\dfrac{W}{12}(L-x)^3-\dfrac{WL^2}{16}(L-x)]
\end{cases}
\]
また、最大たわみ量\(\delta_{max}\)は
\[
\delta_{max}=|\delta(\dfrac{L}{2})|=\dfrac{WL^3}{48EI}
\]
\[
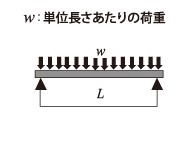M(x)=-\dfrac{w}{2}x^2+\dfrac{wl}{2}
\\
\theta(x)=\dfrac{1}{EI}(-\dfrac{w}{6}x^3+\dfrac{wl}{4}x^2+C_{1})
\\
\delta(x)=\dfrac{1}{EI}(-\dfrac{w}{24}x^4+\dfrac{wl}{12}x^3+C_{1}x+C_{2})
\]
となり、境界条件より
\[
\delta(0)=\dfrac{C_{2}}{EI}=0
\\
\delta(L)=\dfrac{1}{EI}(-\dfrac{wL^4}{24}+\dfrac{wL^4}{12}+C_{1}L)=0
\\
\rightarrow
C_{1}=-\dfrac{wL^3}{24}
\]
よって
\[
\theta(x)=\dfrac{1}{EI}(-\dfrac{w}{6}x^3+\dfrac{wl}{4}x^2-\dfrac{wL^3}{24})
\\
\delta(x)=\dfrac{1}{EI}(-\dfrac{w}{24}x^4+\dfrac{wl}{12}x^3-\dfrac{wL^3}{24}x)
\]
また、最大たわみ量\(\delta_{max}\)は
\[
\delta_{max}=|\delta(\dfrac{L}{2})|=\dfrac{5WL^3}{384EI}
\]