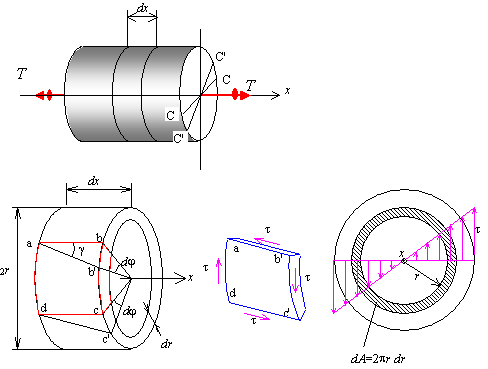
\[ \tau=G\gamma \\ \gamma=\dfrac{\stackrel{\huge\frown}{CC'}}{dx}=r\dfrac{d\phi}{dx} \] 一様な断面を持つ軸では全長を\(l\)、ねじれ角\(\phi\)を用いて \[ \dfrac{d\phi}{dx}=\dfrac{\phi}{l} \\ \tau=G\dfrac{r\phi}{l} \] 仮想断面での中心軸周りのトルクは \[ T=\int dT=\int r\tau dA=\int rG\dfrac{r\phi}{l}dA=G\dfrac{\phi}{l}\int r^2dA \] ここで\(\int r^2dA\)を\(I_{p}\)(断面二次極モーメント)とすると \[ T=G\dfrac{\phi}{l}I_{p}=\dfrac{\tau}{r}I_{p} \] 式変形して \[ \tau=\dfrac{T}{I_{p}/r} \] このとき、仮想断面での最大応力\(\tau_{max}\)は\(r\)が最大のとき(\(r_{max})\)となり \[ \tau_{max}=\dfrac{T}{I_{p}/r_{max}} \] このとき \( \dfrac{I_{p}}{r_{max}} \)を\(Z_{p}\)(極断面係数)とすると \[ \tau_{max}=\dfrac{I_{p}}{Z_{p}} \]